a = np.array([0, 1, 2, 3, 4, 5])
실습을 위한 임의의 배열을 생성하고 이 배열로 이것저것 해보려고 한다.
shape/ndim/size
print("shape: ", a.shape) # 예상 (6, 1)
print("ndim: ", a.ndim) # 예상 2
print("size: ", a.size) # 예상 6
◻ shape : (행, 열)을 뒤집은 형태로 나타냄 → (6, 1) = (1행, 6열)
◻ ndim : 배열 차원
◻ size : 배열의 원소 개수

열이 하나일 경우는 shape에서 1이 찍히지 않는다는 것이 특징! 아직도 차원 개념이 너무 어렵다 ㅠㅠ 텐서 차원이랑 같게 생각해서 스칼라가 1차원, 배열이니까 2차원이라고 생각했는데 1차원이었음. 그냥 파이썬 상의 배열 개념이랑 똑같았다.
shape 인덱싱
# print("shape[1]: ", a.shape[1]) IndexError
print("shape[0]: ", a.shape[0])
print("shape[-1]: ", a.shape[-1])
(6, 1)이니까 shape[-1] 하면 1 나오겠지 했는데 또 사람의 시선으로 생각해버렸다!^^ 행이 하나일 때는 1이 찍히지 않으니까 튜플 요소가 한 개라서 인덱스 0번 원소와 인덱스 -1번 원소가 동일하다.

reshape
a_reshape = a.reshape(3, 2)
print("reshape: ", a_reshape) # 예상
# [[0, 1, 2], [3, 4, 5]
◻ reshape : 행렬의 차원을 원하는 모양으로 바꿀 수 있으며 인자 순서대로 행, 열이다.
◻ reshape 방법 : 기존 배열.reshape(행, 열) / np.reshape(기존 배열, (행, 열))
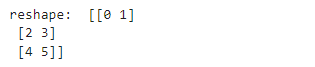
1행 6열의 배열이 3행 2열로 바뀌었다. 예상 결과는 reshape 검색해보고 적은 건데도 틀림
axis
print("axis=0 sum: ", a_reshape.sum(axis=0)) # 행
print("axis=1 sum: ", a_reshape.sum(axis=1)) # 열
sum 함수 인자가 axis=0이면 행 방향으로 요소를 합하고 axis=1이면 열 방향으로 요소를 합한다. 축은 항상 배열보다 작은 값을 갖는다(배열 3차원이면 axis 최댓값은 2).
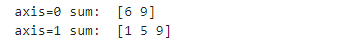
expand_dims
expand_arr = np.array([1, 3])
# expand_dims: 차원 증가
expand_zero = np.expand_dims(expand_arr, axis=0) # [[1, 3]]
expand_one = np.expand_dims(expand_arr, axis=1) # [[1], [3]]
print(f"expand_arr shape: {expand_arr.shape}, expand_arr ndim: {expand_arr.ndim}")
print("axis expand_dims=0: ", expand_zero)
print("axis expand_dims=1: ", expand_one)
print(f"expand_zero shape: {expand_zero.shape}, expand_zero ndim: {expand_zero.ndim}")
print(f"expand_one shape: {expand_one.shape}, expand_one ndim: {expand_one.ndim}")
모를 때는 역시 찍어보는 것이 가장 좋은 방법이라고 생각한다. 위의 코드를 하나씩 풀어서 정리해보면!
- expand_arr : 1차원 배열(ndim=1), shape (2, )
- expand_zero : axis=0이므로 첫 번째 축에 차원 추가, 1행 2열의 2차원 배열
- expand_one : axis=1이므로 두 번째 축에 차원 추가, 2행 1열의 2차원 배열
- expand_zero shape : 첫 번째 축에 차원을 추가했으므로 (1, 2)
- expand_one shape : 두 번째 축에 차원을 추가했으므로 (2, 1)
⭐ expand_dims의 축 차원 추가 개념은 이 곳을 참고했다.

'Artificial Intelligence > 📖' 카테고리의 다른 글
| [정리] Numpy ② : squeeze (0) | 2022.04.20 |
|---|---|
| [정리] train_test_split을 이용한 데이터셋 분할 (0) | 2022.03.17 |
| [개념] 희소 표현 / 밀집 표현 (0) | 2022.03.10 |
| [정리] Encoding 관련 API (0) | 2022.01.28 |
| [개념] object detection 관련 용어 정리 (1) (0) | 2021.11.16 |